December 26, 2017
Siguiendo con las reseñas del libro Writing Great Code, ahora hablaremos un poco sobre lo que ha sido el capítulo 4 en el cual conoceremos básicamente como es que trabaja la representación de punto flotante con nuestro programas o sistemas, ayudándonos también a los problemas que este puede provocar.
Se dice que muchos de los programadores no entienden muy bien este concepto y cuáles son sus limitaciones, por lo que comenzaremos hablando sobre:
¿Qué es la representación del punto flotante?
Contestando a esta pregunta, el libro claramente nos dice que el floating-point (en Ingles) es un aproximado a los números reales. Dice que puede ser un aproximado mas no puede representar a los números reales, pero a los que si puede representar es a los valores fraccionarios.
Además de que el punto flotante puede ser libre de moverse entre la cantidad de números que sean requeridos, por otra también para poder ser representado necesita espacio para poder mostrar el punto.
Un ejemplo de su representación sería el siguiente:
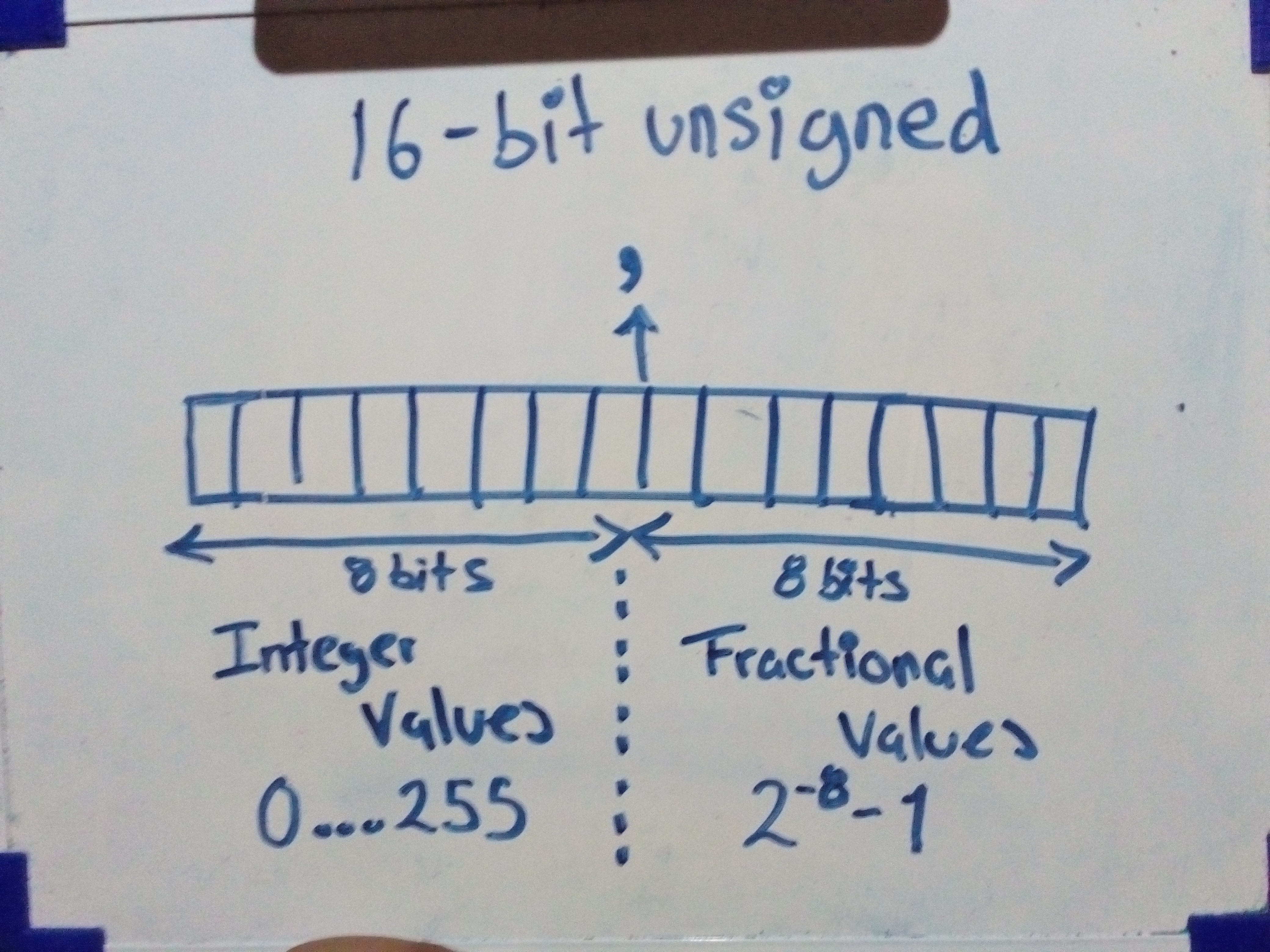
Floating-point se divide de la siguiente forma, entre las cuales sería importante detallar la mantisa, la cual representa los numero que se encuentras a la derecha del punto y el exponte que es representado por una pequeña cantidad de bits.
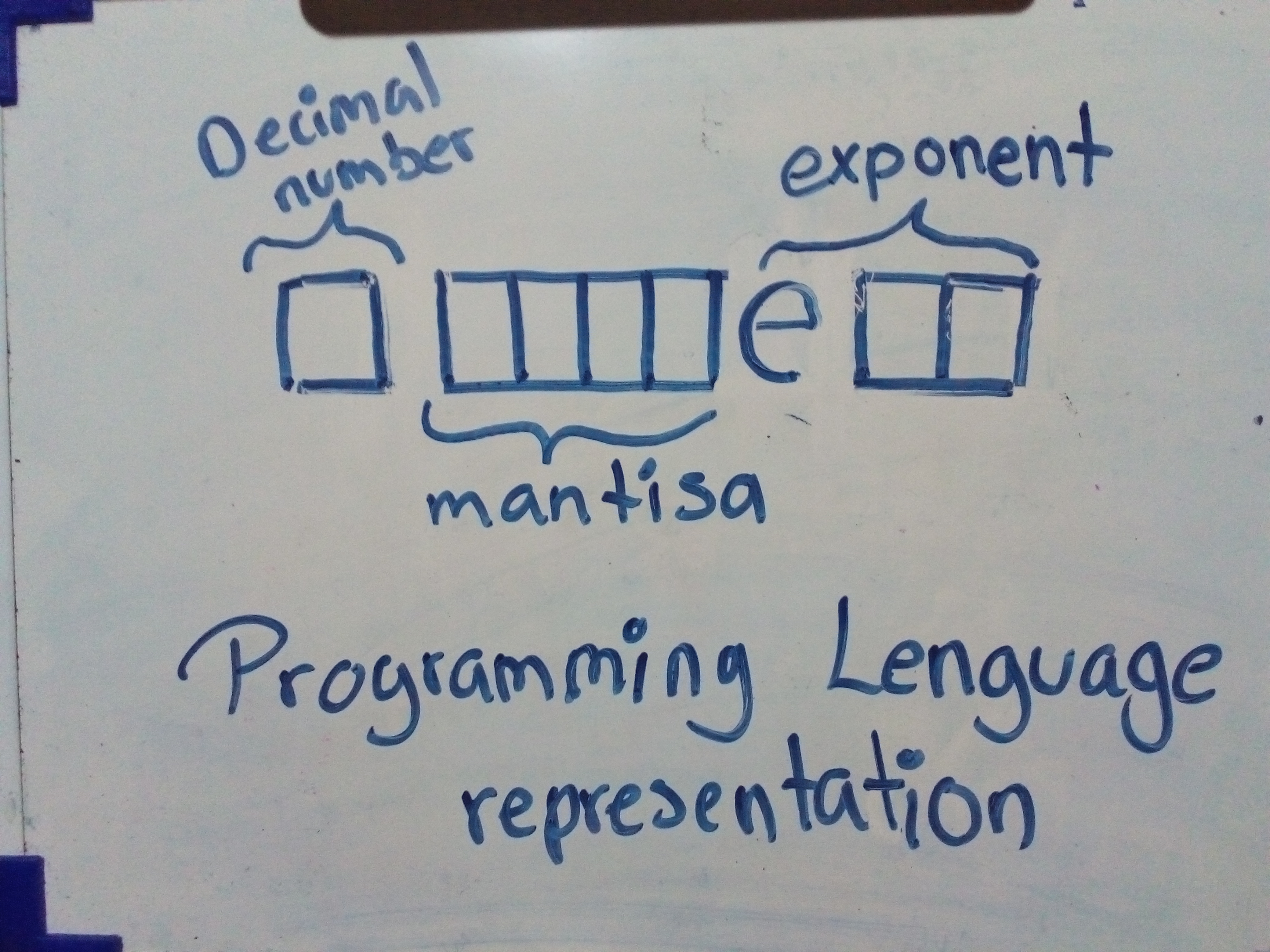
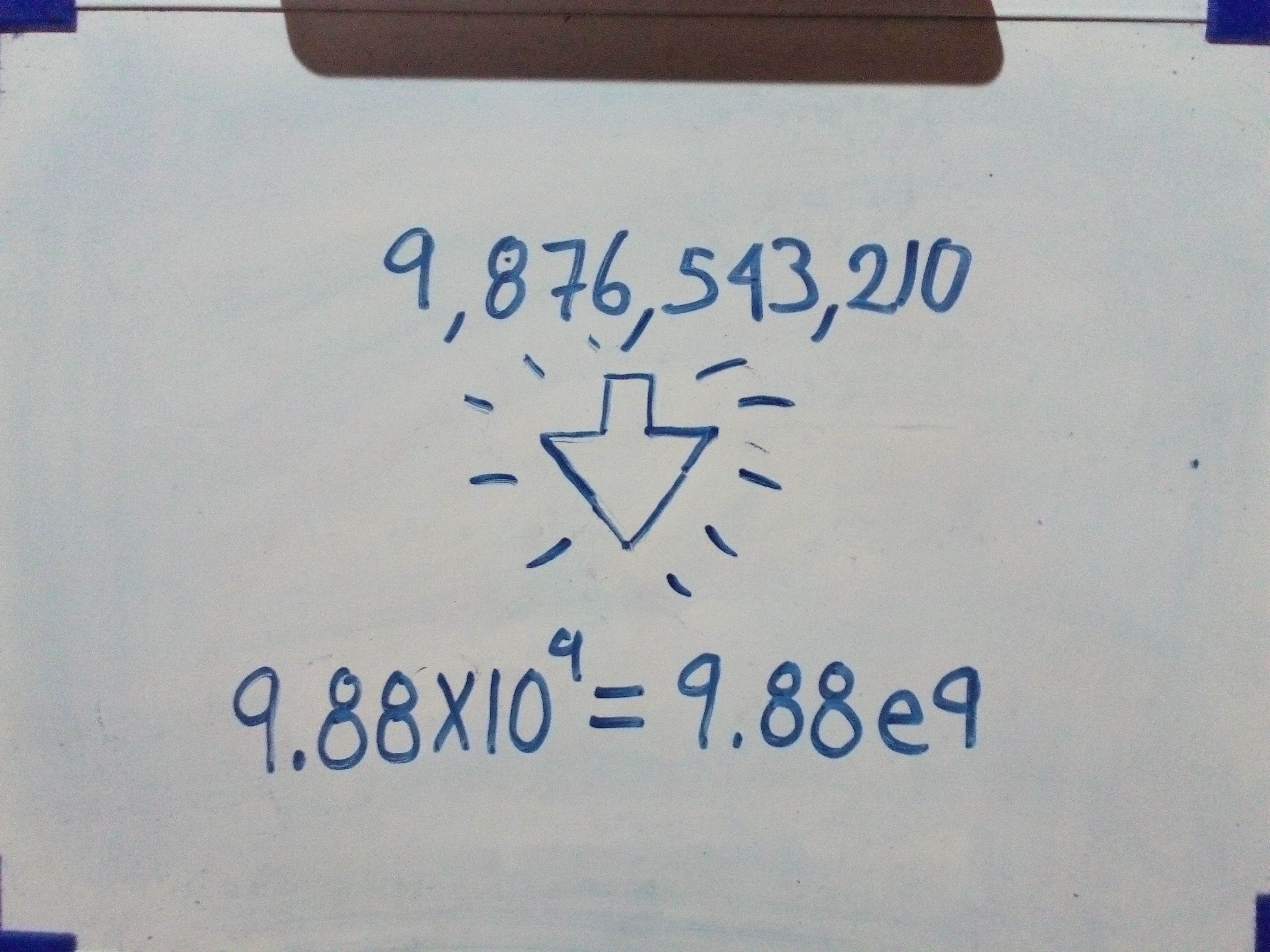
Otro de los aspectos a detallar es que se pueden realizar operaciones con el punto flotante como pueden ser la suma, la resta, la multiplicación y la división las cuales explicare apoyado de un pequeño pizarrón.
Suma

Al redondeado se le llama digito adicional o digito de guarda, esta mejora la precisión de la operación. Por lo que si no se hace puede reducir la precisión del mismo.
Resta
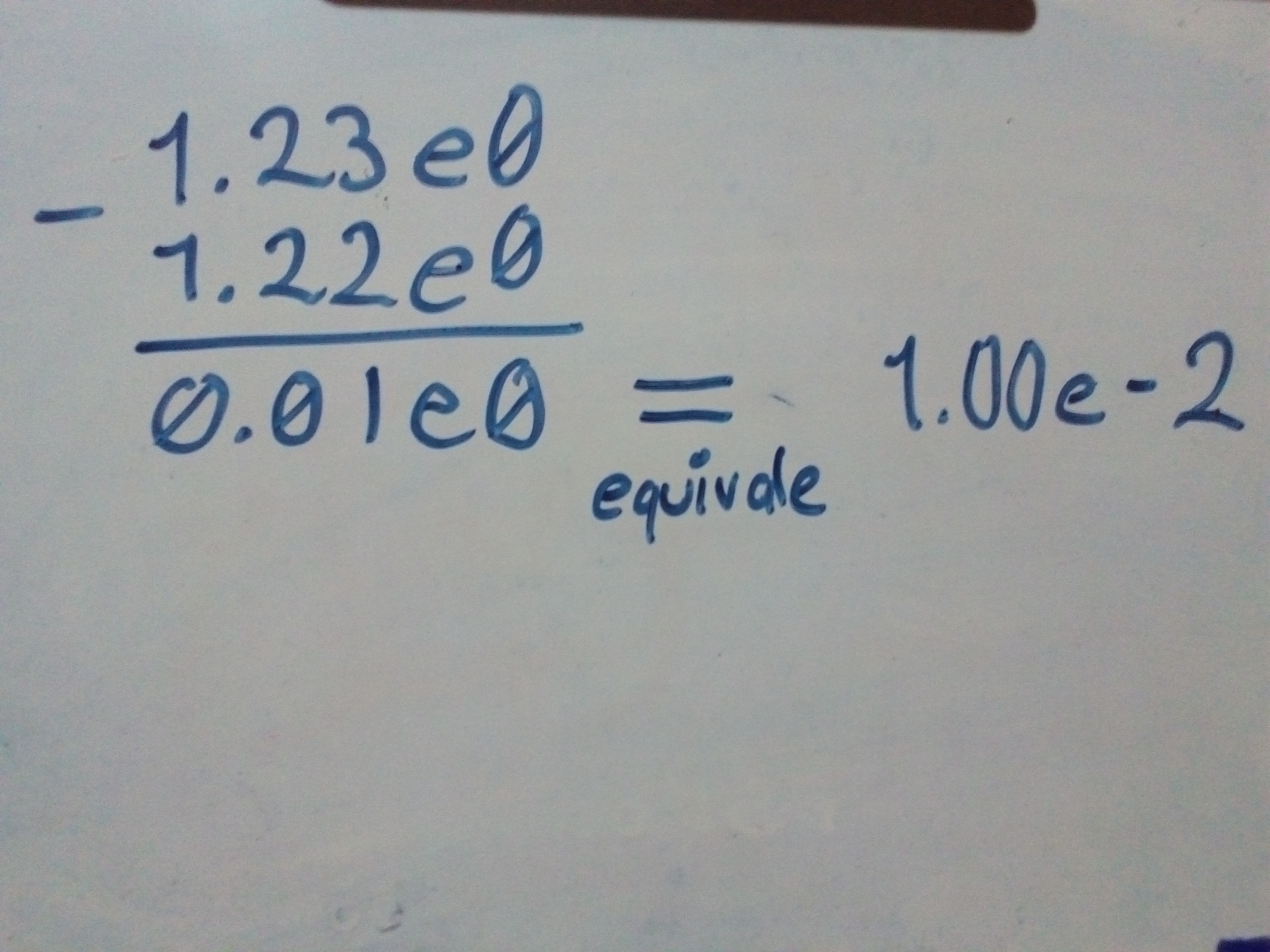
No todas las equivalencias pueden ser exactas debido a que pueden variar con una pequeña diferencia. El resultado en la resta como en la suma también puede mejorar si se igualan las magnitudes (exponentes)
Multiplicación o División
Para realizar la multiplicación y/o división se pueden realizar estas dos opciones:
- Sumar los exponentes y multiplicar las mantisas
- Sustraer el exponente y dividir las mantisas
En el caso de que se hagan operaciones con multiplicaciones y sumas es recomendable realizar primero la multiplicación y después la suma, Ejemplo:
x + (y +z)
(xy)+(xz)
Casos que generan desbordamiento:
- Multiplicar o dividir grandes o pequeños números
- Dividir un número pequeño con uno grande
Es recomendable siempre iguales primeramente las magnitudes para poder tener mayor exactitud en las operaciones.
IEEE Floating-Point Formats
Single Precision Floating Point

- Usa 24-bit divididos en matisa y 8 bit de exponente.
- La mantisa representa un valor de 1o y un poco menos de 2.0.
- El HO siempre estará con un valor de 1 y se representa a la izquierda del punto flotante.
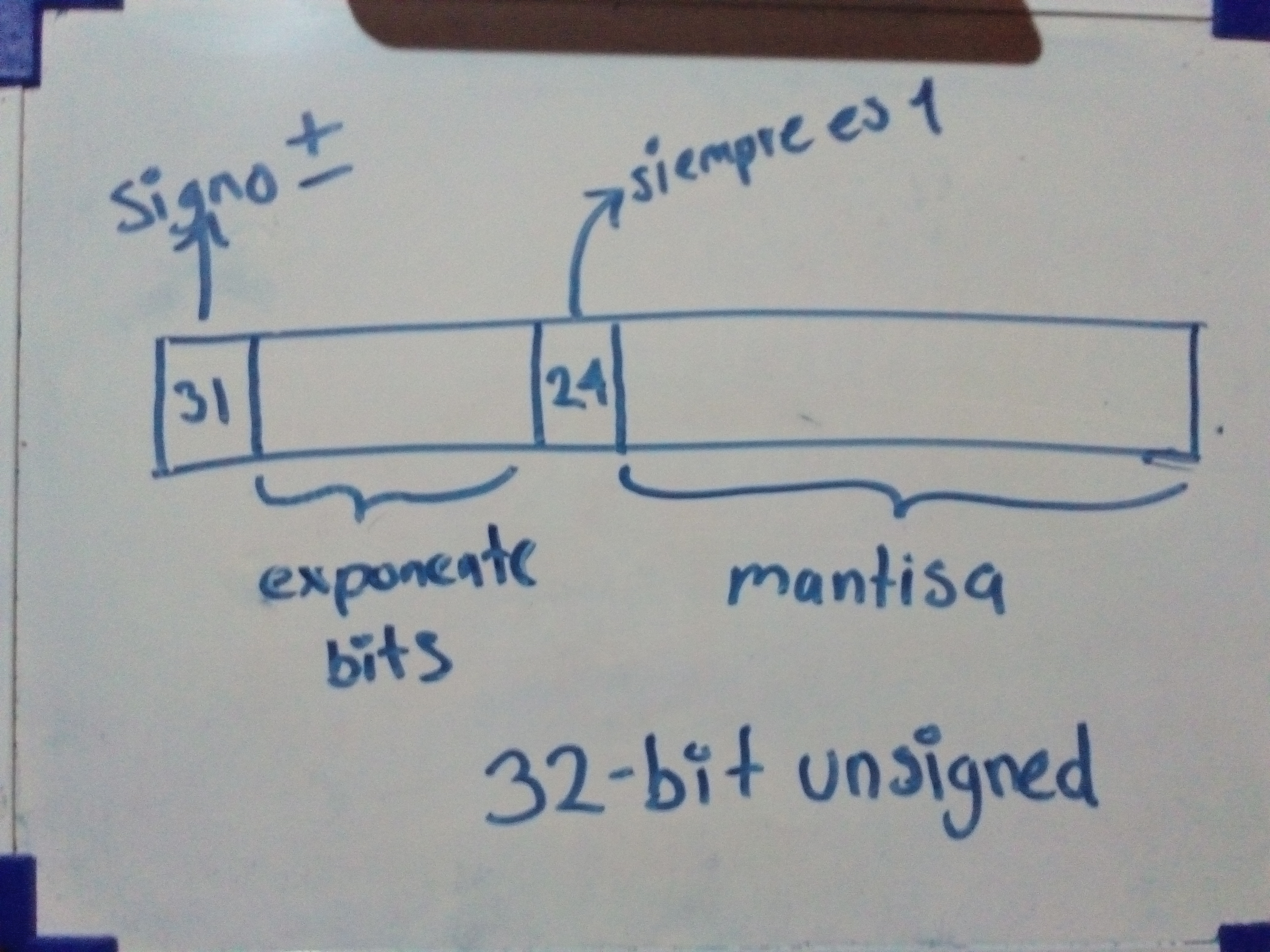
En esta imagen se muestra el caso de 32- bit en el cual se puede observar que el signo se representa en el bit 31, al igual que el de 24-bits en el HO siempre se encontrara el valor 1. Ademas se puede observar que se reserva un espacion para el exponente y la mantisa se sigue manteniendo de la misma forma.
Double Precision
El formato de doble precisión ayuda a superar los problemas del punto flotante de precisión simple. Utilizando el doble de espacio.
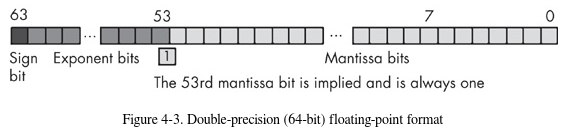
Se puede observar que el exponente ocupa un espacio de 11 bits, mientras que la mantisa 53 bits incluyendo un bit HO implícito de uno y un bit de signo.
Extend Precision
Este esta hecho para soportar largas cadenas que involucran números de coma flotante de precisión doble.
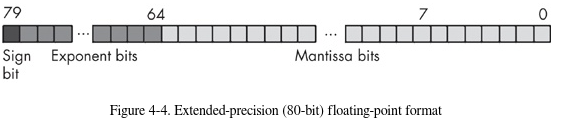
Este formato a diferencia de los otros no tiene un bit HO que siempre sea uno. Por lo tanto, el formato de precisión extendida cuenta con una mantisa de 64 bits la cual esta dividida en 2 partes al igual que el de doble precision, 15 bits para el exponente y un bit para el signo.
Normalización y Desnormalización de Valores
La normalización nos ayudara a tener mayor precisión en nuestros valores. De hecho, cuando un bit HO contiene un 1 significa que mantiene el máximo número de bits de precisión, mientras que cuando un valor que se encuentra desnormalizado no lo está. Pero para ello este número se puede Normalizar desplazando los bits mantisa hacia la izquierda y disminuyendo su exponente hasta que aparezca un “1” en el bit HO de la mantisa.
Ejemplo:
0.100000 x 21 --------> 1.00000 x 20
Existen algunas excepciones como:
- No se puede normalizar el cero debido a que no podrá contener ningún 1 como bit.
- Cuando tenemos solamente ceros en la mantisa y nuestro exponente es 0
Redondeo
El redondeo siempre nos dará mejor precisión en cualquiera de las operaciones que realicemos. Aunque en el caso de los números negativos para poder aumentar redondear se necesita reducir nuestro exponente, debido a que esto ayudara a que se agregue un bit a nuestra operación en la parte de LO de la mentisa ayudando a completar nuestro redondeo.
Valores especiales del Punto Flotante
Existen distintas excepciones que son lanzadas por algunos de nuestros compiladores a la hora de trabajar con números flotantes por lo cual resumiré esta parte a través de una gráfica en la cual se ordenan de menor a mayor riesgo a la hora de que estas son mostradas.

Por último, cabe mencionar que todo esto nos puede ayudar a entender como es que funciona el punto flotante, saber cuales son sus debilidades y poder tomar acciones en base a ellas a la hora de escribir código.
Si llegarás a tener alguna duda con respecto al post o piensas que se podría mejorar la explicación en algun apartado con gusto puedes contactarme y escribirme.